简单分析并使用 Java 语言实现常见排序、查找算法，以及十余种其他较为经典的算法。

部分算法实现代码较为简单，不再列出。

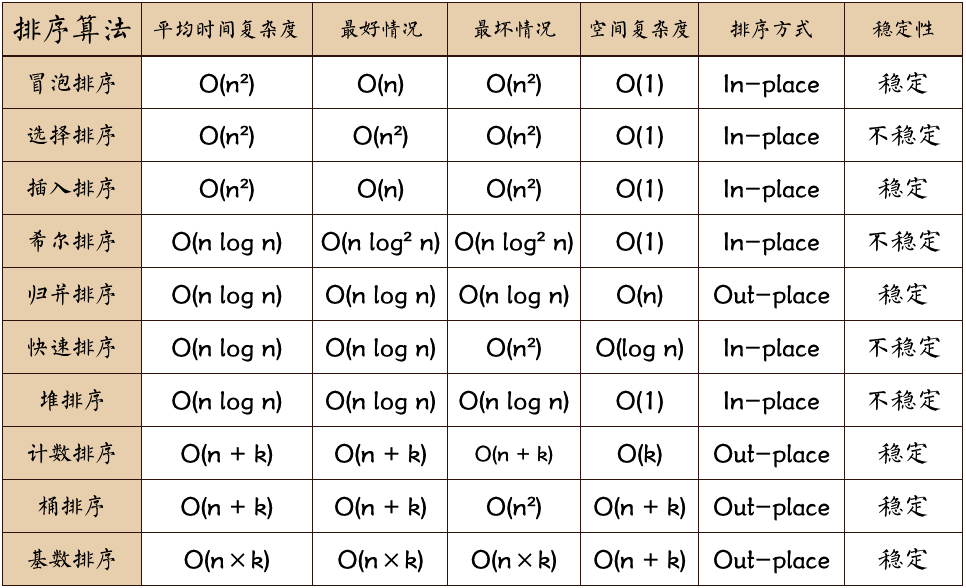
排序算法

• 本节所涉及算法代码的实现效果为将数组升序排列（从小到大）。
• 针对 i 从 1 到 10 的循环，i=1 的循环体完成表述为一次，从 1 到 10 全部完成表述为一轮。

交换排序

冒泡排序

从左至右，相邻元素两两比较，发现逆序则交换；内循环遍历完一轮后，目标值就“冒泡”到了最右侧；下次外循环针对的数组元素值减 1。

Tip：如果数组本身已经有序，原始的冒泡排序仍然会进行与无序时相同的遍历次数；此时可以设置 flag 标记，记录单轮内循环是否发生过交换，如果没有发生过则证明排序已经完成，可直接结束。

快速排序

使用递归实现。先选择一个中间值，通过交换（中间值左侧的一个大值，右侧的一个小值）这样一对元素，实现将比其小的元素都放到左边，比其大的元素都放到右边，然后对左右分别再递归计算。

注意点是【单侧先交换完，没有跟另一侧配对元素时】的处理方法。

import java.util.Arrays;

public class QuickSort {

    public static void main(String[] args) {    //测试排序效果，下文与此类似不再给出
        int[] a = {1, 3, 4, 9, 1, 6, 6, 8, -1};
        System.out.println(Arrays.toString(a));
        sort(a);
        System.out.println(Arrays.toString(a));
    }

    public static void sort(int[] a) {     //实现不带参方法
        sortWithArgs(a, 0, a.length - 1);
    }

    private static void sortWithArgs(int[] array, int start, int end) {
        if (start >= end) {
            return;
        }

        int middle = partition01(array, start, end); // 这里可选不同的目标值，partition01 取中间（类似二分）
        //int middle = partition01(array, start, end); //partition02 直接取最左侧

        sortWithArgs(array, start, middle - 1);   //左右侧分别递归
        sortWithArgs(array, middle + 1, end);
    }

    private static void partition01(int[] array, int start, int end) {
        int middle = (start + end) / 2;
        int left = start;
        int right = end;
        int tmp;

        while (left < right) {      //左右分别向中间值逼近
            while (array[left] < array[middle]) {   //不加等于条件，保证不越过middle
                left++;
            }
            while (array[middle] < array[right]) {
                right--;
            }
            if (left < right) {     //发现有一对不符要求的就交换
                tmp = array[left];
                array[left] = array[right];
                array[right] = tmp;
                if (left == middle) {   //如果左侧先配对完毕
                    middle = right;     //上面的配对已经导致 middle 到了 right 位置
                    left++;             //继续比较
                } else if (right == middle) {   //右侧同理
                    middle = left;
                    right--;
                }

                if (array[left] == array[right]) {  //此 if 成立时，left/right/middle 处数组值相等
                left++;                             //手动跨过
                right--;
                }
            }
        
        }
    }

    private static void partition02(int[] array, int start, int end) {
        int tmp = array[start];
        while(start < end) {
            while(start < end && array[end] >= tmp) end--;
            array[start] = array[end];
            while (start < end && tmp >= array[start]) start++;
            array[end] = array[start];
        }
        arr[start] = tmp;
        return start;
    }
}

选择排序

简单选择排序

与冒泡排序类似。不同的是在简单选择排序中，目标元素固定在最右侧，每轮内循环会遍历目标元素前的元素并找到最大值，与目标元素交换，实现与“冒泡”相同的结果；下次外循环针对的数组元素值减 1。

堆排序

对于一个完全二叉树，如果任意节点值都大于等于其子节点的值，则称此完全二叉树为大顶堆；若小于等于，则称为小顶堆。大顶堆根节点值必为最大值。

堆排序先将数组排序为大顶堆，然后将位置 1 元素（即根节点）与位置 n-1 元素交换，再对前 n-2 个元素依此执行，实现每轮的最大值都排至队尾，最终实现从小到大排序。

import java.util.Arrays;

public class HeapSort {
    
    public static void sort(int[] a) {
        for (int i = a.length / 2 - 1; i >= 0; i--) {   //先通过循环将数组排列为大顶堆
            adjustHeap(a, i, a.length);                 //调整以 i 为父节点的子树
        }

        for (int j = a.length - 1; j > 0; j--) {
            int temp = a[0];    //完成首尾元素交换
            a[0] = a[j];
            a[j] = temp;    //此时根节点（位置 0）左右子树仍满足大顶堆，但根节点不满足

            adjustHeap(a, 0, j);
        }
    }

    /**
     * 在以 i 为父节点的子树均为大顶堆的前提下，实现根节点 i 的大顶堆
     *
     * @param a      数组
     * @param i      要实现的大顶堆的根节点
     * @param length 待排序数组长度（数组末尾已排好的元素不计入）
     */
    private static void adjustHeap(int[] a, int i, int length) {
        int temp = a[i];    //记录此次调整的根节点

        for (int k = i * 2 + 1; k < length; k = k * 2 + 1) {
            if (k + 1 < length && a[k] < a[k + 1]) {
                k++;    //每次循环 k 先指向左子节点，通过 if 指向左右子节点中的较大者
            }

            if (a[k] > temp) {
                a[i] = a[k];
                i = k;
            } else {
                break;
            }
        }

        a[i] = temp;
    }
}

插入排序

直接插入排序

对于第 i 个元素 a[i]，a[i] 及其之前的元素均为有序排列，之后的为无序。将 a[i+1] 插入合适位置，使 a[i+1] 及其之前元素均实现有序，依此循环遍历即可。

import java.util.Arrays;

public class InsertSort {

    public static void sort(int[] a) {
        int tmp;        //待插入的元素
        boolean flag;   //标记是否插入成功，若循环完毕还未成功，说明要插到索引 0 位置

        for (int i = 0; i < a.length - 1; i++) {
            flag = false;
            tmp = a[i + 1];
            for (int j = i; j >= 0; j--) {  //依次与前置元素比较
                if (tmp < a[j]) {           //若小于某前置元素，则要与更前置的元素比较
                    a[j + 1] = a[j];        //但由于要向前插，此此次比较的元素位置要后移
                } else {
                    a[j + 1] = tmp;         //否则就说明插入此位置
                    flag = true;
                    break;                  //不必担心此位置原来元素丢失，已经在前次内循环时后移
                }
            }
            if (!flag) {
                a[0] = tmp;                 //如果一轮内循环结束都未插入成功，直接插至首位
            }
        }
    }
}

希尔排序

考虑原始数组越接近降序情况时，使用直接插入排序完成升序排列，元素要移动的次数越多。

希尔（Shell）排序可以减少一些不必要的移动，实现改进，实现思路是：初始先用大步长，分组进行排序；然后步长逐步减小至 1，同时分组数逐步增大至数组长度，最后一轮是直接插入排序。

import java.util.Arrays;

public class ShellSort {
   
    public static void sort(int[] a) {
        boolean flag;   //标记是否插入成功，若循环完毕还未成功，说明要插到本组第一个位置
        int tmp;        //待插入的元素

        for (int gap = a.length / 2; gap > 0; gap /= 2) {   //gap 为步长，每次缩小为原来一半
            for (int i = 0; i < a.length - gap; i++) {      //第一个步长内元素，作为各组的起始位置
                flag = false;
                tmp = a[i + gap];
                for (int j = i; j >= 0; j -= gap) {         //与直接插入类似，不同的是步长为 gap
                    if (tmp < a[j]) {
                        a[j + gap] = a[j];
                    } else {
                        a[j + gap] = tmp;
                        flag = true;
                        break;
                    }
                }
                if (!flag) {
                    a[i % gap] = tmp;
                }
            }
        }
    }
}

归并排序

采用典型的“分治”策略。

“分”阶段：每次将数组分成 2 份，对每一小份再分成 2 份，依此循环，直至每小份只有一个元素。

“治”阶段：倒退回去，每次两两合并，每次合并可以看作是两个各自有序小数组 -> 一个整体有序大数组

import java.util.Arrays;

public class MergeSort {

    public static void sort(int[] a) {      //实现不带参方法
        sortWithArgs(a, 0, a.length - 1, new int[a.length]);
    }

    private static void sortWithArgs(int[] a, int left, int right, int[] temp) {
        if (left < right) {
            int mid = (left + right) / 2;
            sortWithArgs(a, left, mid, temp);                 //左子列实现排序
            sortWithArgs(a, mid + 1, right, temp);       //右子列实现排序
            merge(a, left, mid, right, temp);                 //左右归并，合成有序大数组
        }
    }

    private static void merge(int[] a, int left, int mid, int right, int[] temp) {
        int i = left;           //i 是左子列起始
        int j = mid + 1;        //j 是右子列起始
        int tempPointer = 0;    //temp 是辅助数组，缓存排序好的元素，tempPointer 指示缓存到的位置
        while (true) {          //先去看 else 分析
            if (i > mid) {      //如果左子列首先全部放入 temp
                for (; j <= right; j++) {   //将右子列剩余值全部放入 temp
                    temp[tempPointer++] = a[j];
                }
                for (int p = left, q = 0; p <= right; p++, q++) {
                    a[p] = temp[q];     //将 temp 中排序好的元素依次放回数组 a
                }
                break;
            } else if (j > right) {     //如果右子列首先全部放入 temp
                for (; i <= mid; i++) {
                    temp[tempPointer++] = a[i];
                }
                for (int p = left, q = 0; p <= right; p++, q++) {
                    a[p] = temp[q];
                }
                break;
            } else {    //左右子列分别比较，小值放入temp
                if (a[i] > a[j]) {
                    temp[tempPointer++] = a[j++];
                } else {
                    temp[tempPointer++] = a[i++];
                }
            }
        }
    }
}

基数排序

预先设置代表 0~9 的总计 10 个桶，将数组中的数字从低位到高位逐位分析；先看个位数，依次放到各个桶中，按序取出后得到的数组已经按照个位数排序；再看十位数，以此类推直到最高位。

import java.util.Arrays;

public class RadixSort {
    public static void main(String[] args) {    //注意，数组不能出现负数
        int[] a = {1, 453, 4, 249, 11, 6562, 623, 88, 0};
        System.out.println(Arrays.toString(a));
        sort(a);
        System.out.println(Arrays.toString(a));
    }

    public static void sort(int[] a) {
        int max = a[0];
        for (int i : a) {   //循环找到最大值的位数
            if (i > max) max = i;
        }
        int maxLength = Integer.toString(max).length();

        int[][] buckets = new int[10][a.length];    //定义 10 个桶，按最大容量定义
        int[] flags = new int[10];                  //标记每个桶存储到了哪个位置

        for (int i = 0; i < maxLength; i++) {       //按照位数循环
            Arrays.fill(flags, 0)   //先将标记置为 0

            for (int j = 0; j < a.length; j++) {    //遍历数组 a，取出对应位上的数
                int num = a[j] / (int) Math.pow(10, i) % 10;
                buckets[num][flags[num]] = a[j];    //放入相应的桶
                flags[num]++;                       //标记更新
            }

            int index = 0;
            for (int j = 0; j < buckets.length; j++) {      //遍历桶
                for (int k = 0; k < flags[j]; k++) {        //根据标记位置
                    a[index++] = buckets[j][k];             //将桶中数据放回原数组
                }
            }
        }
    }
}

总结

图源：十大经典排序算法最强总结（含JAVA代码实现）

查找算法

线性查找

较为简单，不再赘述。

二分查找

较为简单，不再赘述。

插值查找

二分查找的进阶版，可以理解为【按照数组为均匀分布的假设去查找】。

对数组 a，目标值 target 以及左右边界索引 l 和 r，不再每次简单取中间索引 $mid = (l + r) / 2$，而按下式取值：

可以分析，当数组完全均匀时，查找效率最高，几乎一次命中。

斐波那契查找

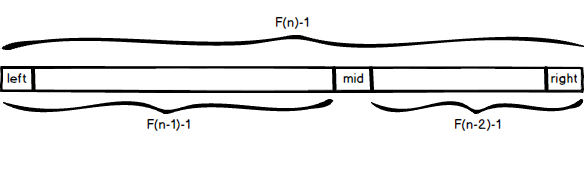
插值查找的进阶版，又称“黄金分割查找”，是黄金分割率的典型应用。

数据均匀分布是一种理想情况，即假想数据按固定步长增长；在没有其他信息的情况下，数据增长步长假设按黄金分割增长更加合理。可以证明，斐波那契数列相邻两项之比的极限值即为黄金分割比值。

对斐波那契数列 F(n)，有 F(n) = F(n-1) + F(n-2)，即 F(n)-1 = [F(n-1)-1] + [F(n-2)-1] + 1 。

因此对一个长度为 F(n)-1，左右边界索引为 left 和 right 的数组，每次循环取中间索引： mid = left + F(n-1) - 1 。

import java.util.Arrays;

public class FibonacciSearch {
    public static void main(String[] args) {
        int[] a = {1, 453, 4, 249, 11, 6562, -6, 623, 88, 0};
        System.out.println(Arrays.toString(a));
        Arrays.sort(a);
        System.out.println(Arrays.toString(a));
        System.out.println(search(a, 6562));
    }

    public static int search(int[] a, int target) {
        int[] fib = getFib(10);
        int k = 0;  //记录斐波那契数列的索引值
        while (a.length > fib[k] - 1) {
            k++;    //将原数列扩展至fib[i]-1
        }
        int[] newArrary = Arrays.copyOf(a, fib[k] - 1);

        for (int i = a.length; i < newArrary.length; i++) {
            newArrary[i] = a[a.length - 1];     //多余位置以最大值填充
        }

        int l = 0;
        int r = newArrary.length - 1;
        int mid;
        do {
            mid = l + fib[k - 1] - 1;     //关键取值
            if (newArrary[mid] > target) {
                k--;    //左半部分
                r = mid - 1;
            } else if (newArrary[mid] < target) {
                k -= 2; //右半部分
                l = mid + 1;
            } else {
                if (mid < a.length) {   //检测是否后来的填充部分
                    return mid;
                } else {
                    return a.length - 1;
                }
            }
        } while (l <= r);

        return -1;
    }

    public static int[] getFib(int size) {  //获取长度为size的斐波那契数列
        int[] fib = new int[size];
        if (size < 3) {
            System.out.println("斐波那契数列过小");
            return null;
        }
        fib[0] = 1;
        fib[1] = 1;
        for (int i = 2; i < size; i++) {
            fib[i] = fib[i - 1] + fib[i - 2];
        }
        return fib;
    }
}

其他算法

回溯

回溯算法是类似数学中的排列思想，穷举所有可能的状况（易错点是容易忘记“还原现场”步骤）。由于时间复杂度多为指数级，对回溯类题目，应考虑是否能应用动态规划，降低时间复杂度。

动态规划

动态规划是很典型的递归思想，即某一步的计算结果，需要依赖上一步的计算结果，也即需要一个关键的递推公式，以及保存中间结果的 DP 数组。典型动态规划问题包括常规问题（斐波那契额数列、爬楼梯）、打家劫舍、背包问题等，可有“记忆化搜索”与“递推”两种实现方式（一说记忆化搜索不属于动态规划，但二者思想亦基本一致）。

以打家劫舍问题为例，题目描述可点击至力扣网查看，简单来说，就是求非负数列中任意个成员的最大和，其中这任意个成员两两不能相邻，即如果计入了 a[i]，则 a[i-1] 和 a[i+1] 就都不能计入求和。

首先，最容易想到的点就是“递归”。由于数值均为非负数，对长度为 n 的数组 a，记 t(i) 为索引从 i 至 n-1 的子序列的最高金额，则 t(i) = max(t(i+1), a[i]+t(i+2))，即为递推公式（注意：最高金额 t(i) 并不意味着一定要将 a[i] 计算进去）。代码如下：

class Solution {
    private int[] memo;

    public int rob(int[] nums) {
        return rob(nums, 0);
    }

    private int rob(int[] nums, int startIndex) {
        if(startIndex >= nums.length) return 0;
        return Math.max(nums[startIndex] + rob(nums, startIndex + 2), rob(nums, startIndex+1));
    }
}

然而上述代码显然非常不合理，原因是递归过程中出现了很多重复计算，极大地降低了效率，在力扣部分测试用例甚至会超时。很容易想到的办法就是把中间结果保存起来，如果已经计算过某个中间结果，就直接取出该结果，即为“记忆化搜索”，用来保存中间结果的数据结构即为 DP 数组。优化代码如下：

class Solution {
    private int[] memo;

    public int rob(int[] nums) {
        memo = new int[nums.length];
        Arrays.fill(memo, -1);
        return rob(nums, 0);
    }

    private int rob(int[] nums, int startIndex) {
        if(startIndex >= nums.length) return 0;
        if(memo[startIndex] == -1) memo[startIndex] = Math.max(nums[startIndex] + rob(nums, startIndex + 2), rob(nums, startIndex + 1));
        return memo[startIndex];
    }
}

进一步观察上述逻辑，可以看到我们是从索引 0 开始向后计算，但对每一步计算的索引 i，都用到了 i 后面的结果，且直观上只用到了 i 后两位的结果。因此猜想，如果从索引 n-1 开始向前计算，则只保留最近两次中间结果即可，同时又自然而然地避免了重复计算，即为“递推”。此时也可能用循环来代替递归，代码如下（与斐波那契数列十分相似）：

class Solution {
    public int rob(int[] nums) {
        int n = nums.length;
        if(n == 1) return nums[0];

        int res = Math.max(nums[n-2], nums[n-1]), lastRes = nums[n-1], tmp; //res 和 lastRes 保存中间结果，可以视作 DP 数组
        for(int i=n-3; i>=0; i--) {
            tmp = Math.max(res, nums[i] + lastRes);
            lastRes = res;
            res = tmp;
        }
        return res;
    }
}

可以看出，“记忆化搜索”与“递推”方法的思想类似，在计算起止方向上有所不同。

“选或不选”还是“选哪个”

以“最长递增子序列问题”为例。假设从右向左递推，有两种思路：

1. 对于第 i 个元素选或者不选，取决于上一个选取的元素（因为要保证严格递增），有 nums[i]>=pre 时，f(i, pre) = f(i-1, pre)；否则 f(i, pre) = max(f(i-1, pre), f(i-1, nums[i]) + 1)。此时时间复杂度 O(n)，空间复杂度 O(n^2)

2. 对于第 i 个元素已选，需要遍历 i 位置之前的元素，f(i) = max(f(j)) + 1，其中 j 需满足 nums[j] < nums[i]。此时时间复杂度 O(n^2)，空间复杂度 O(n)

可以看出二者是时间空间的选择问题。对于其他此类问题，思路 2 的空间、时间复杂度一般不会变化，而思路 1 的空间复杂度则变化较大。例如这里提到的“最长递增子序列问题”，为了保证严格递增，pre 的可能取值是 nums 的每个元素，即严格依赖，因此两种思路各有优劣（一般选择思路 2）；而例如问题“访问数组中的位置使分数最大”，只需依赖上个元素的奇偶性。对这种弱依赖甚至不依赖的问题，空间复杂度一般也是 O(n)，因此一般选择思路 1。

贪心算法

贪心算法是一种说简单也简单，说难也难的算法，核心思想就是“以局部最优推导全局最优”。要实现全局最优解，就拆分步骤，使得每步都是局部最优解。该算法省去了穷举带来的资源耗费，缺点是不能完全保证“最优”，只能接近最优（在某些情况下，也可以推导出贪心算法就是最优解）。

以“找零钱”为例，假设找给顾客 41 元钱，面值有 25 元、20 元、10 元、5 元和 1 元，每个面值都有多张。为了实现尽量少的找零钱张数，我们每步只找一张，每张都找符合要求的最大面值，因此依次找给顾客 25 元、10 元、5 元、1 元，就是贪心思想。但显然，两张 20 元和一张 1 元是最优解，此情况下贪心不能保证最优。

以力扣网的“分发饼干”为例（题目描述至原文查看），我们将小孩和饼干都按从小到大排序，然后同时便利，以期用尽量小的饼干满足每一个小孩。利用反证法，假设某一步，贪心算法选择了质量为 x 的饼干（这是满足这个孩子的最小的饼干），假设非贪心算法选择另一个质量为 y 的饼干（可知 y>x），则下一步的待选小孩与贪心算法一样，但饼干却有一个不一样（质量原可以为 y，却成了 x），则后续解只会与贪心相同或者更差。同理也可分析固定饼干，小孩选择不同时的情况。因此此题贪心算法就是最优解。

本质上，贪心与其说是一种算法，更接近是一种思想。以前述两题为例，二者在思路上除了“不选大的怎么能赢”（注：炉石酒馆 Bob 的台词）的贪心思想外，实际相似之处并不多，也就是说并没有固定的思路。“分发饼干”可以严格证明，可以说这次的所谓贪心是成熟正确的算法；而“找零钱”的贪心结果本就不是最优，更无从证明（实际分析一下，找零金额从 0 向 41 元递增，类似背包问题，用上小节的动态规划可能更好）。认为“找零钱”的贪心不是真正的贪心算法，或者是错误地使用了贪心算法，某种意义上也都是可行的，而且也确实接近了最优解。因此，学会这种贪心的思想是更重要的。

并查集

并查集实际上是一种数据结构，非常适用于求解多个集合关系的问题，主要有初始化、合并、查询这三个关键实现。详细可查看博文。

前缀和

前缀和非常适用于求解子串/子数组问题，本质是由索引 i 和 j 处的前缀和信息，推导出片段 [i: j] 的子信息。经典题目见“和为 K 的子数组”

参考

• 灵茶山艾府 合集·基础算法精讲 高频面试题
• 技术面试必备知识点